

If we examine the classical equations for gravitation, electrical force, and sound energy at a distance, we find they all have a factor in common:
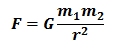
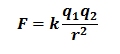
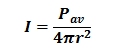
The r2 in the denominators are examples of inverse square laws. It's just a simple matter of geometry. Imagine a point source of light in the center of a sphere with a radius of r. The surface area of the sphere is 4πr2. The amount of light passing through a unit area of the sphere will be total light divided by the surface. If you double the distance, the surface area is squared in comparison and the light must fall on and be divided by a surface that is proportional to the square of the distance.
Astronomers use a stellar magnitude scale to describe the brightness of astronomical objects. The star Vega is assigned an apparent magnitude of 0. A fifth magnitude star is 100 times dimmer and a -5 magnitude object would be 100 times brighter. This is a logarithmic scale, much as the decibel scale is used for sound, in order to account for the eye's non-linear response to light.
| Magnitude | Example | x Vega | Magnitude | Example | x Vega | Magnitude | Example | x Vega |
|---|---|---|---|---|---|---|---|---|
| -27 | Sun | 63 billion | 1 | Antares | .398 | 12 | Visual Limit of 3" telescope | .1.58 x 10-5 |
| -12.7 | Full Moon | 120,200 | 2 | Polaris | .158 | 13.7 | Visual Limit of 6" telescope | 3.31 x 10-6 |
| -7.5 | SN1006 | 1000 | 3 | Mergrez (dimmest dipper star) | .0631 | 14.4 | Visual Limit of 8" telescope | 1.74 x 10-6 |
| -6 | SN1054 (Crab) | 251 | 4 | αCnc | .0251 | 14.9 | Visual Limit of 10" telescope | 1.1 x 10-6 |
| -5 | Venus (max) | 100 | 5 | Uranus (max) | .01 | 15.6 | Visual Limit of 14" telescope | 5.75 x 10-7 |
| -3 | Jupiter, Mars (max) | 15.8 | 6 | Naked eye limit | .00398 | 18.5 | ~photographic limit of my telescope | 3.98 x 10-8 |
| -2 | Mercury (max) | 6.31 | 7 | Ceres (max) | .00158 | 22.2 | Visual limit of Mt. Palomar | 1.318 x 10-9 |
| -1 | Sirius | 2.51 | 8 | Neptune (max) | 6.31 x 10-4 | 27 | Visual limit of 8m telescope | 1.58 x 10-11 |
| 0 | Vega, Saturn (max) | 1 | 9 | 2.51 x 10-4 | 32 | Visual limit of Hubble | 1.58 x 10-13 |
Although I am in the country 35 miles from Des Moines, my location suffers a little light pollution and there is perhaps a 10% extinction from the haze of jets since we sit under several major fly-ways. A thirty minute exposure gets me to about 18.5 magnitude with my 10 inch Newtonian.

NGC2264, jet wing lights, and fuselage strobe on 2-15-13 -- Rick Whitten
Absolute magnitude is a measure of a star's intrinsic brightness. The standard is the apparent magnitude that a star would have if placed at 10 parsecs. A parsec is one parallax-second.The parallax of a star is the shift of a nearby star in its apparent position against background stars when measured 6 months apart. Thus the Earth's orbital radius forms one side of a right triangle and trigonometry gives the star's distance. A parsec is the distance at which the shift is one second of arc -- about 3.26156 light years.
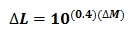
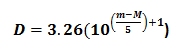
Using the inverse square law and a little arithmetic and we can transform the luminosity equation into a distance equation. Given a limiting magnitude (m) and an absolute magnitude (M), I can calculate how far an object can be seen. Main sequence stars are the most common (each followed by "V" after their color) and the have a pretty well determined absolute magnitude. So, here's how far I can see, how far you can see with the naked eye, and how far the Hubble telescope can see.
| Class | Temperature | Mass | Abs Mag | Naked eye distance | My telescope/camera | Hubble distance |
|---|---|---|---|---|---|---|
| O5V | 39,000 K | 60 | -5.4 | 6200 ly | 1.96 million ly | 1 billion ly |
| B0V | 28,000 K | 17.5 | -3.7 | 2840 ly | 900,000 ly | 450 million ly |
| B5V | 6,000 K | 5.9 | -1 | 820 ly | 260,000 ly | 130 million ly |
| A0V | 9,900 K | 2.9 | .6 | 390 ly | 124,000 ly | 62 million ly |
| A5V | 8,650 K | 1.9 | 1.9 | 215 ly | 68,000 ly | 34 million ly |
| F0V | 7,400 K | 1.6 | 2.6 | 156 ly | 49,000 ly | 25 million ly |
| F5V | 6,700 K | 1.4 | 3.4 | 108 ly | 34,000 ly | 17 million ly |
| G0V | 6,600 K | 1.1 | 4.3 | 71 ly | 22,500 ly | 11 million ly |
| G5V | 5,450 K | 0.9 | 5.2 | 47 ly | 14,900 ly | 7.5 million ly |
| K0V | 4,900 K | 0.8 | 5.9 | 34 ly | 10,800 ly | 5.4 million ly |
| K5V | 4,200 K | 0.7 | 7.2 | 18.7 ly | 5,900 ly | 2.9 million ly |
| M0V | 3,500 K | 0.5 | 9.0 | 8.2 ly | 2,600 ly | 1.3 million ly |
| M5V | 2,667 K | 0.2 | 14.6 | .62 ly | 196 ly | 98,000 ly |
| M0Ia0 | 3,700 K | 15.8 | -9.3 | 37,500 ly | 11.8 million ly | 6 billion ly |
| F8Ia | 6,280 K | 8.5 | -7.9 | 19,600 ly | 6.2 million ly | 3.1 billion ly |
| SN Type II | >8 | -17 | 1.2 million ly | 410 million ly | 13.8 billion ly | |
| SN Type Ia | 1.4 | -19 | 3.26 million ly | 1.03 billion ly | 13.8 billion ly |
Recall from The Color of Stars that the M class stars are the most common main sequence stars. Note that even Hubble can't see them in the nearby Andromeda galaxy which is 2.5 million light years away. But Red supergiants (M0Ia0)and supergiants in general (listed at the bottom) are visible to Hubble one eighth the way across the universe. A type Ia supernova might be visible in the Andromeda galaxy to the naked eye. Supernovas would not be necessarily be visible to Hubble at the edge of the universe (13.8 billion light years) because of extinction and redshift. I am quite pleased that my camera turns my modestly small telescope into a semi-respectable astronomical instrument.